கெப்ளரின் விதிகளை அறிவோம்!
-----------------------------------------------------------------
நியூட்டன் அறிவியல் மன்றம்
---------------------------------------------------------------
( முந்தைய பதிவில் உள்ள கணக்கும் அதன் விடையும்)
------------------------------------------------------------------------------------------------
சரியான விடையும் விளக்கமும்!
----------------------------------------------------------
சூரியனில் இருந்து பூமி 15 கோடி கி.மீ
தூரத்தில் உள்ளது. இதில் பாதி தூரத்தில்
பூமி இருப்பதாக கற்பனை செய்தால்,
ஓராண்டு எத்தனை நாட்களைக் கொண்டதாக இருக்கும்?
தற்போது ஓராண்டுக்கு 365 நாள் என்று கொள்க.
விளக்கம்: இந்தக் கணக்கை கெப்ளரின் Law of periods
விதியைக் கொண்டு செய்ய வேண்டும்.
**
Law of periods: The square of the period of revolution of any planet is
proportional to the cube of the planet's mean distance from the sun.
Therefore, T^2 is directly proportional to R^3.
**
சூரியனைச் சுற்றுகிற எந்த ஒரு கோளின்
சுழற்சிக்காலத்தின் வர்க்கமானது, சூரியனுக்கும்
அக்கோளுக்கும் உள்ள சராசரி தூரத்தின்
மும்மடிக்கு நேர்விகிதப் பொருத்தத்தில் இருக்கும்.
இதுதான் மேற்கூறிய கெப்ளரின் விதியின் தமிழாக்கம்.
**
இப்போது கணக்கைச் செய்யலாம்.
சூரியன்-பூமி தூரம்= R என்க. (R = 15 கோடி கி.மீ= 1 AU)
காலம் = Time Period= T என்க. (T = 365 நாட்கள்)
சூரியன்-பூமி புதிய தூரம் = a என்க (a = 7.5 கோடி கி.மீ = 0.5 AU)
இதற்கான காலம் = b என்க. (இதைக் கண்டறிய வேண்டும்).
**
கெப்ளரின் விதிப்படி,
b^2 /T^2 = a^3/R^3
b^2/ 365^2 = 0.5^3/1^3
On simplifying we get, b= 129 days.
எனவே, சூரியனுக்கும் பூமிக்கும் இடையிலான தூரம்
பாதியாகக் குறையுமானால், ஒரு ஆண்டு என்பது
129 நாட்களாக இருக்கும்.
*********************************************************
-----------------------------------------------------------------
நியூட்டன் அறிவியல் மன்றம்
---------------------------------------------------------------
( முந்தைய பதிவில் உள்ள கணக்கும் அதன் விடையும்)
------------------------------------------------------------------------------------------------
சரியான விடையும் விளக்கமும்!
----------------------------------------------------------
சூரியனில் இருந்து பூமி 15 கோடி கி.மீ
தூரத்தில் உள்ளது. இதில் பாதி தூரத்தில்
பூமி இருப்பதாக கற்பனை செய்தால்,
ஓராண்டு எத்தனை நாட்களைக் கொண்டதாக இருக்கும்?
தற்போது ஓராண்டுக்கு 365 நாள் என்று கொள்க.
---------------------------
விடை: 129 நாட்கள்.விளக்கம்: இந்தக் கணக்கை கெப்ளரின் Law of periods
விதியைக் கொண்டு செய்ய வேண்டும்.
**
Law of periods: The square of the period of revolution of any planet is
proportional to the cube of the planet's mean distance from the sun.
Therefore, T^2 is directly proportional to R^3.
**
சூரியனைச் சுற்றுகிற எந்த ஒரு கோளின்
சுழற்சிக்காலத்தின் வர்க்கமானது, சூரியனுக்கும்
அக்கோளுக்கும் உள்ள சராசரி தூரத்தின்
மும்மடிக்கு நேர்விகிதப் பொருத்தத்தில் இருக்கும்.
இதுதான் மேற்கூறிய கெப்ளரின் விதியின் தமிழாக்கம்.
**
இப்போது கணக்கைச் செய்யலாம்.
சூரியன்-பூமி தூரம்= R என்க. (R = 15 கோடி கி.மீ= 1 AU)
காலம் = Time Period= T என்க. (T = 365 நாட்கள்)
சூரியன்-பூமி புதிய தூரம் = a என்க (a = 7.5 கோடி கி.மீ = 0.5 AU)
இதற்கான காலம் = b என்க. (இதைக் கண்டறிய வேண்டும்).
**
கெப்ளரின் விதிப்படி,
b^2 /T^2 = a^3/R^3
b^2/ 365^2 = 0.5^3/1^3
On simplifying we get, b= 129 days.
எனவே, சூரியனுக்கும் பூமிக்கும் இடையிலான தூரம்
பாதியாகக் குறையுமானால், ஒரு ஆண்டு என்பது
129 நாட்களாக இருக்கும்.
*********************************************************

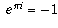 . So I put it into the calculator and it worked, but I have no idea why, because e to any power isnt supposed to be a negative number, and I thought pi was in no way related to e.If you could explain the process, it would save lots of time pondering and plugging e, pi, and i into the calculator in random ways to figure out whats going on.
. So I put it into the calculator and it worked, but I have no idea why, because e to any power isnt supposed to be a negative number, and I thought pi was in no way related to e.If you could explain the process, it would save lots of time pondering and plugging e, pi, and i into the calculator in random ways to figure out whats going on.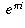 even mean?" In other words, what does it mean to raise a number to an imaginary power?
even mean?" In other words, what does it mean to raise a number to an imaginary power?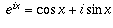 for all x, a fact which is known as de Moivre's formula, and illustrates how closely related the exponential function is to the trigonometric functions. From this formula, it follows immediately that
for all x, a fact which is known as de Moivre's formula, and illustrates how closely related the exponential function is to the trigonometric functions. From this formula, it follows immediately that 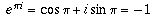 .
.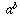 means "a multiplied by itself b times." That definition only makes sense when b is a positive integer. After all, what would it mean to multiply something by itself i times??
means "a multiplied by itself b times." That definition only makes sense when b is a positive integer. After all, what would it mean to multiply something by itself i times??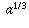 to be that number which, if you raise it to the power of 3, would give you
to be that number which, if you raise it to the power of 3, would give you 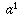 (i.e., a); in other words,
(i.e., a); in other words, 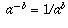 .
.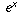 happens to be equal to the infinite sum
happens to be equal to the infinite sum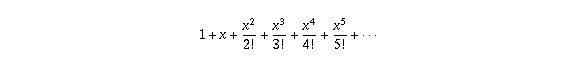
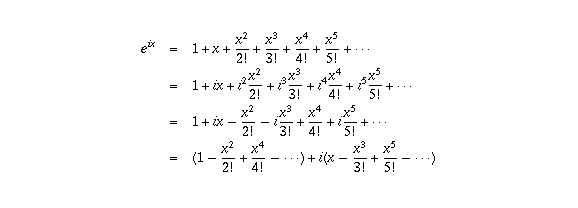
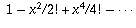 is the infinite sum for cos x, while
is the infinite sum for cos x, while 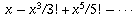 is the infinite sum for sin x (again by the theory of Taylor series). Therefore,
is the infinite sum for sin x (again by the theory of Taylor series). Therefore, 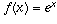 , f(x) may represent, for example, an exponentially growing population. The rate of change of such a population (the number of births per day, for example) is directly proportional to the current size of the population; that is, f'(x) is a constant times f(x). When
, f(x) may represent, for example, an exponentially growing population. The rate of change of such a population (the number of births per day, for example) is directly proportional to the current size of the population; that is, f'(x) is a constant times f(x). When 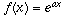 , then
, then 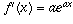 .
.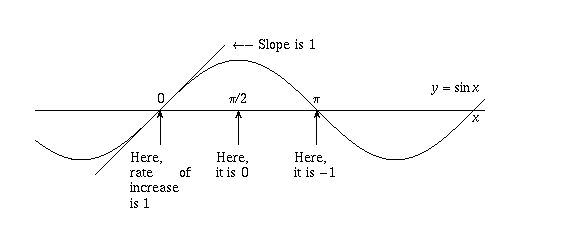
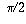 , the rate of increase drops off and eventually sin x stops increasing altogether and starts decreasing. In other words, f'(x) drops to zero when
, the rate of increase drops off and eventually sin x stops increasing altogether and starts decreasing. In other words, f'(x) drops to zero when 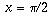 , and becomes -1 by the time x reaches pi (see the picture).
, and becomes -1 by the time x reaches pi (see the picture).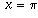 , rises back to 0 when
, rises back to 0 when 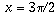 , and so on. This is precisely what the cosine function does, so it should be no surprise that f'(x) = cos x. Similar reasoning shows why it is reasonable that, when f(x)=cos x, f'(x)=-sin x. The exact proofs of these facts you will see in a calculus class.
, and so on. This is precisely what the cosine function does, so it should be no surprise that f'(x) = cos x. Similar reasoning shows why it is reasonable that, when f(x)=cos x, f'(x)=-sin x. The exact proofs of these facts you will see in a calculus class.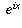 be? If we write it in terms of real and imaginary parts g(x) + i h(x), what should the functions g(x) and h(x) be?
be? If we write it in terms of real and imaginary parts g(x) + i h(x), what should the functions g(x) and h(x) be?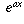 should still equal
should still equal 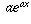 . Therefore, if
. Therefore, if 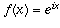 , we should have
, we should have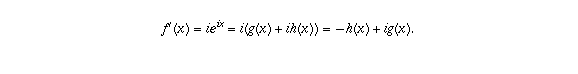
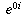 needs to equal 1, uniquely determine the functions g and h.
needs to equal 1, uniquely determine the functions g and h.