Why is e^(pi i) = -1?
Asked by Brad Peterson, student, Roy High on January 29, 1997:I was watching an episode of The Simpsons the other day, the one where Homer gets sucked into the third dimension, and in this 3-D world, there was an equation that saidWe'd be glad to explain; that's exactly what this area is here for.. So I put it into the calculator and it worked, but I have no idea why, because e to any power isnt supposed to be a negative number, and I thought pi was in no way related to e.If you could explain the process, it would save lots of time pondering and plugging e, pi, and i into the calculator in random ways to figure out whats going on.
The first question to ask, though, is not "why does
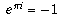 ", but rather, "what does
", but rather, "what does 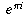 even mean?" In other words, what does it mean to raise a number to an imaginary power?
even mean?" In other words, what does it mean to raise a number to an imaginary power?Once that question is answered, it will be much more clear why
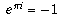 . It turns out that
. It turns out that 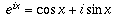 for all x, a fact which is known as de Moivre's formula, and illustrates how closely related the exponential function is to the trigonometric functions. From this formula, it follows immediately that
for all x, a fact which is known as de Moivre's formula, and illustrates how closely related the exponential function is to the trigonometric functions. From this formula, it follows immediately that 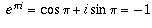 .
.So now, the question is, why is
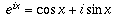 the "right" thing to define what e raised to an imaginary power means?
the "right" thing to define what e raised to an imaginary power means?Raising a number to an imaginary power makes no sense based on the original definition of exponentiation you learned, where
 means "a multiplied by itself b times." That definition only makes sense when b is a positive integer. After all, what would it mean to multiply something by itself i times??
means "a multiplied by itself b times." That definition only makes sense when b is a positive integer. After all, what would it mean to multiply something by itself i times??Of course, the original definition doesn't even make sense for fractions and negative numbers. You should have learned how to extend the definition to include fractions. For example, since 1/3 is that number which, when multiplied by 3, gives you 1, it makes sense to define
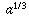 to be that number which, if you raise it to the power of 3, would give you
to be that number which, if you raise it to the power of 3, would give you 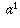 (i.e., a); in other words,
(i.e., a); in other words, 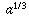 is defined to be the cube root of a. Similarly, you learned how to extend the definition to negative exponents by
is defined to be the cube root of a. Similarly, you learned how to extend the definition to negative exponents by 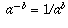 .
.But none of these considerations give any clue as to what raising a number to a complex power should mean. Instead, we need to express exponentiation, or its properties, in some way that can be extended to complex powers.
The first way to do this is to use the fact that
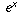 happens to be equal to the infinite sum
happens to be equal to the infinite sum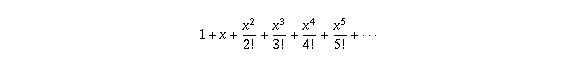
(where n! means n factorial, the product of the numbers 1,2,. . . ,n).
The reason why this is so depends on the theory of Taylor series from calculus, which would take too long to describe here. You will encounter it in a calculus class at some point, if you haven't already.
Now, this infinite sum makes perfectly good sense even for imaginary numbers. By plugging in ix in place of x, you get
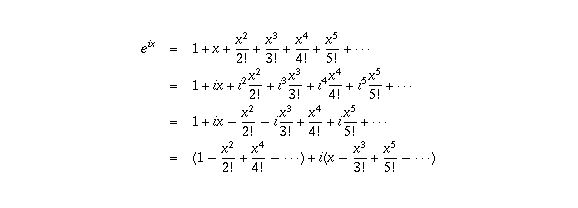
Now it turns out that
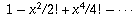 is the infinite sum for cos x, while
is the infinite sum for cos x, while 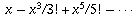 is the infinite sum for sin x (again by the theory of Taylor series). Therefore,
is the infinite sum for sin x (again by the theory of Taylor series). Therefore, 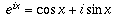 .
.Now, this may be a little unsatisfying to you since I haven't explained why
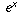 , cos x, and sin x equal those three different infinite sums. I can't do so without assuming some calculus background that you may not have.
, cos x, and sin x equal those three different infinite sums. I can't do so without assuming some calculus background that you may not have.However, here's another way of understanding why
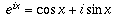 . It too involves some calculus, but I can describe the calculus involved more easily.
. It too involves some calculus, but I can describe the calculus involved more easily.Associated to many functions f(x) is another function f'(x), called the derivative of f(x). It measures how rapidly f(x) is changing at the value x.
If
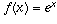 , f(x) may represent, for example, an exponentially growing population. The rate of change of such a population (the number of births per day, for example) is directly proportional to the current size of the population; that is, f'(x) is a constant times f(x). When
, f(x) may represent, for example, an exponentially growing population. The rate of change of such a population (the number of births per day, for example) is directly proportional to the current size of the population; that is, f'(x) is a constant times f(x). When 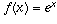 , that constant is exactly 1 (that's the property which defines the number e). More generally, if
, that constant is exactly 1 (that's the property which defines the number e). More generally, if 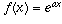 , then
, then 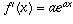 .
.What about the trigonometric functions? Well, if f(x) = sin x, then f'(x) = cos x, and if f(x) = cos x, then f'(x) = - sin x.
If you think about it for a minute, these equations are very reasonable. First of all, when x=0, sin x equals zero but increases as x increases; in fact, the slope of the graph of y = sin x at the point (0,0) is 1, which is another way of saying that the rate of increase there is 1, so f'(0) = 1.
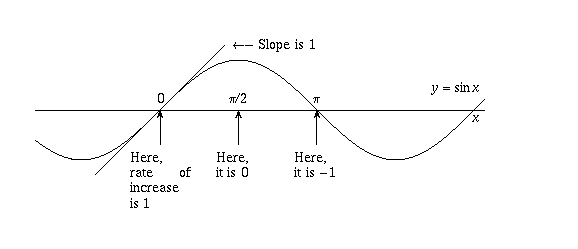
But then, as x increases to
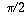 , the rate of increase drops off and eventually sin x stops increasing altogether and starts decreasing. In other words, f'(x) drops to zero when
, the rate of increase drops off and eventually sin x stops increasing altogether and starts decreasing. In other words, f'(x) drops to zero when 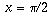 , and becomes -1 by the time x reaches pi (see the picture).
, and becomes -1 by the time x reaches pi (see the picture).Therefore, f'(x) is a function which starts at 1 when x=0, decreases to 0 when
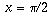 , drops to -1 when
, drops to -1 when 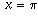 , rises back to 0 when
, rises back to 0 when 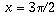 , and so on. This is precisely what the cosine function does, so it should be no surprise that f'(x) = cos x. Similar reasoning shows why it is reasonable that, when f(x)=cos x, f'(x)=-sin x. The exact proofs of these facts you will see in a calculus class.
, and so on. This is precisely what the cosine function does, so it should be no surprise that f'(x) = cos x. Similar reasoning shows why it is reasonable that, when f(x)=cos x, f'(x)=-sin x. The exact proofs of these facts you will see in a calculus class.Now, keeping those facts in mind, what should
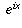 be? If we write it in terms of real and imaginary parts g(x) + i h(x), what should the functions g(x) and h(x) be?
be? If we write it in terms of real and imaginary parts g(x) + i h(x), what should the functions g(x) and h(x) be?The key is to take the derivative. It is only reasonable to define
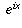 in such a way that it still has the same properties as mentioned above, namely, the derivative of
in such a way that it still has the same properties as mentioned above, namely, the derivative of 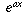 should still equal
should still equal 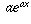 . Therefore, if
. Therefore, if 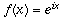 , we should have
, we should have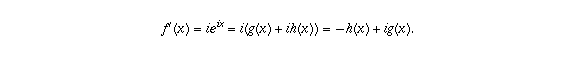
But f'(x) should also equal g'(x) + i h'(x), so we are looking for a pair of functions g and h for which h' = g and g' = -h. This is exactly the same interrelationship that the sine and cosine functions have, as we saw above. It also turns out that these two equations, together with the conditions g(0)=1 and h(0)=0 that arise from the fact that
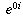 needs to equal 1, uniquely determine the functions g and h.
needs to equal 1, uniquely determine the functions g and h.It follows from all this that g must be the cosine function and h must be the sine function. That is why
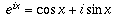 .
.
கருத்துகள் இல்லை:
கருத்துரையிடுக